2014-12-29
10:00-11:00
FAMNIT-SEMIN
prof. dr. Vladimir Gurvich (Rutgers University, USA)
On Nash-solvability of chess-like games
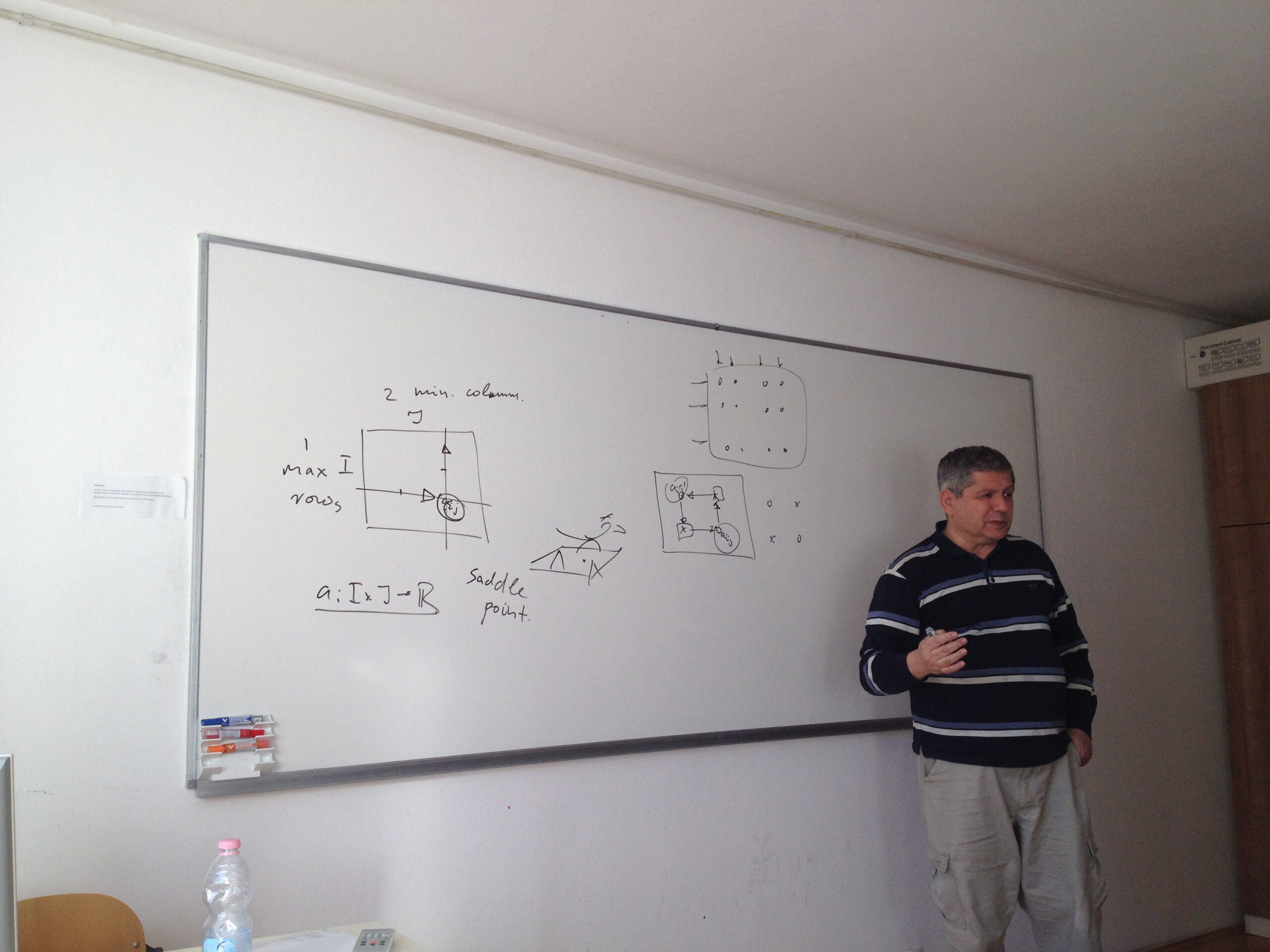
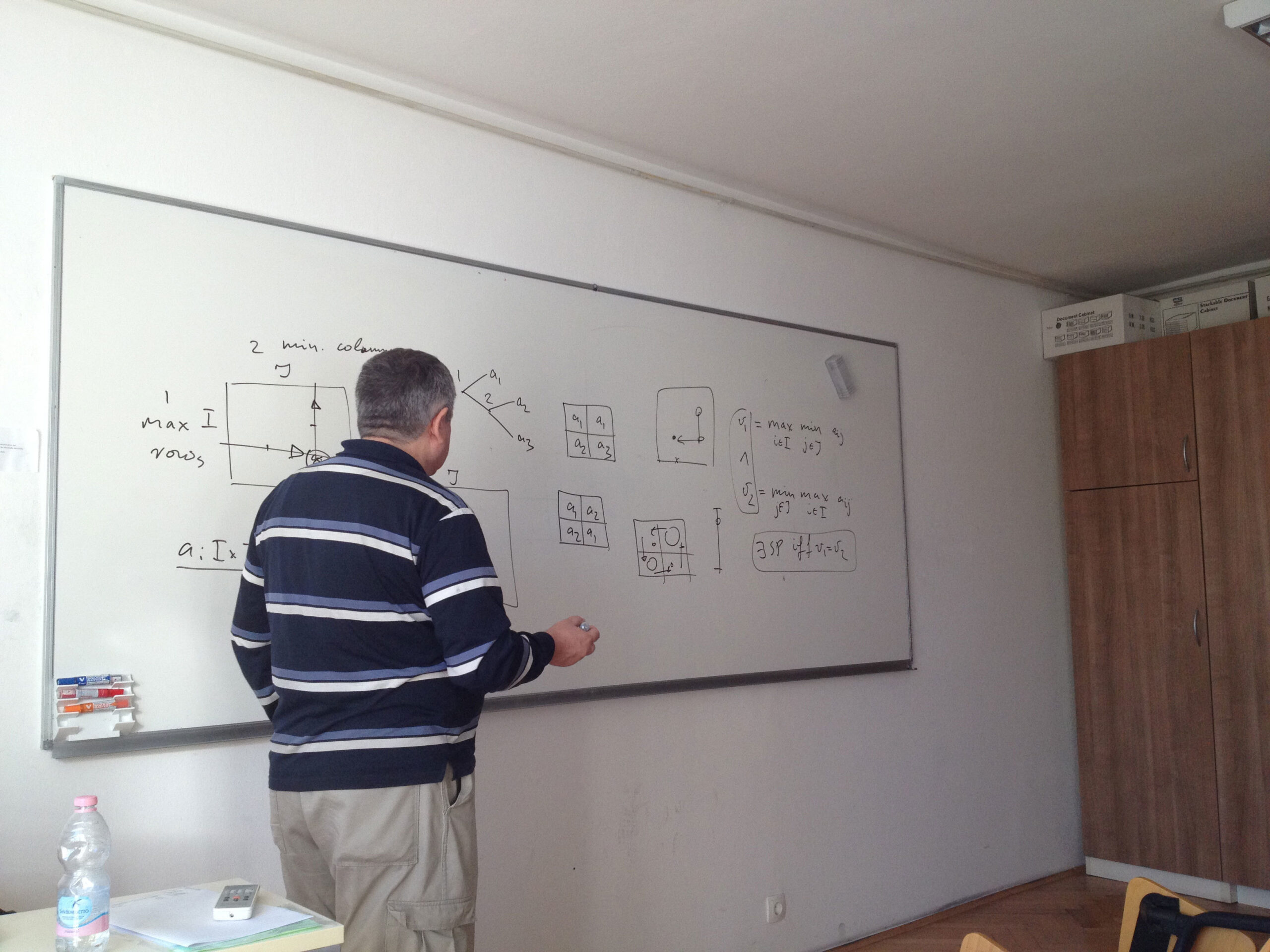
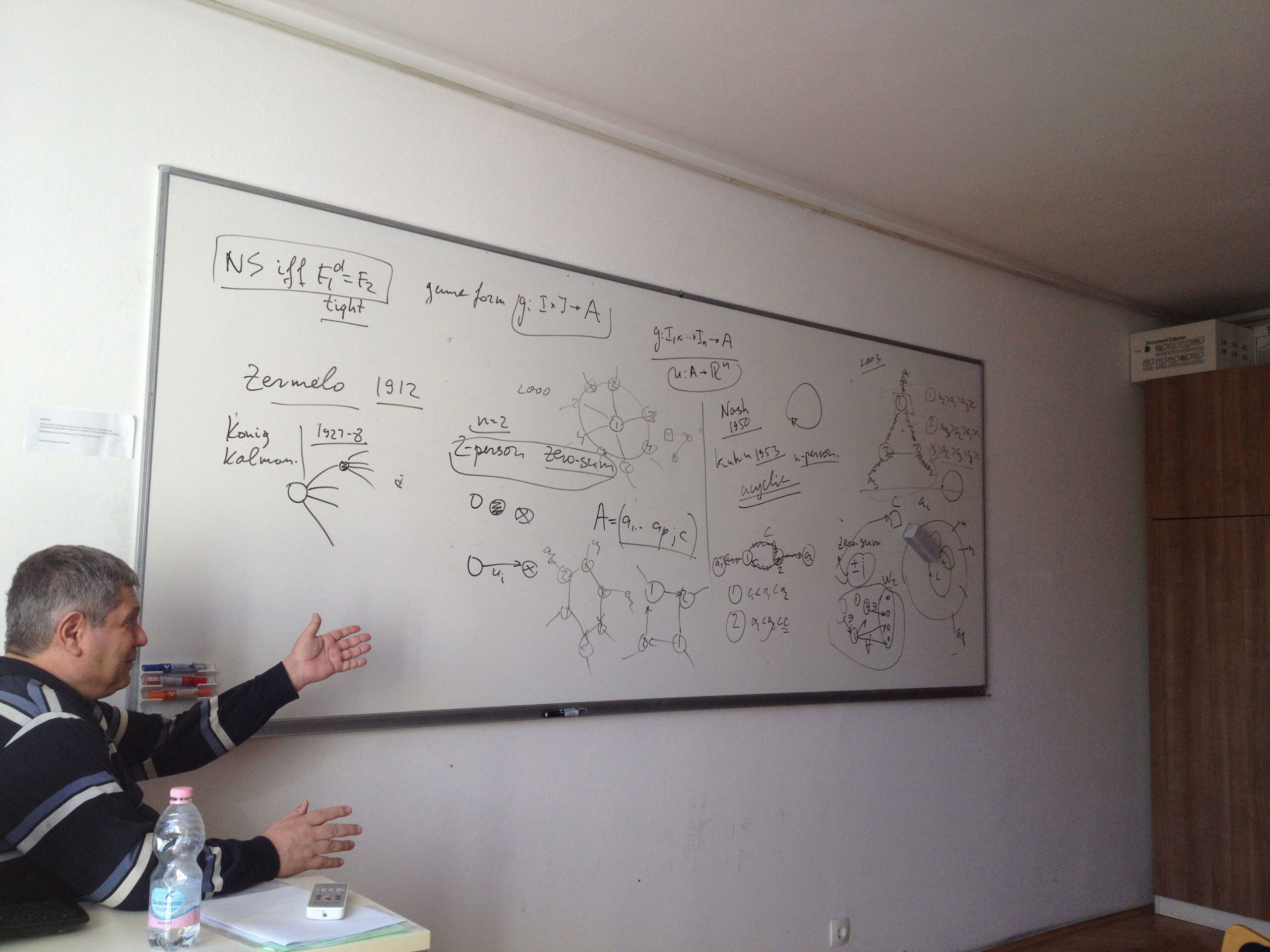
In 2003, Boros and Gurvich proved that a chess-likes game has a Nash equilibrium (NE) in pure stationary strategies if (A) the number n of players is at most 2, or (B) the number p of terminals is at most 2 and (C) any infinite play is worse than each terminal for every player. In the talk we strengthen the bound in (B) replacing p <= 2 by p <= 3, provided (C) still holds. On the other hand, we construct an NE-free four-person chess-like game with five terminals, which has a unique cycle, but does not satisfy (C). It remains open whether an NE-free example exists for n = 3, or for 2 < p < 4, or for some n > 3 and p > 4 provided (C) holds.
Joint work with E. Boros, V. Oudalov, and R. Rand.