Univerza na Primorskem Fakulteta za matematiko, naravoslovje in informacijske tehnologije
2018-12-03
10:00-11:00
FAMNIT-MP7 (formerly FAMNIT-POŠTA)
Tomaž Pisanski (University of Primorska)
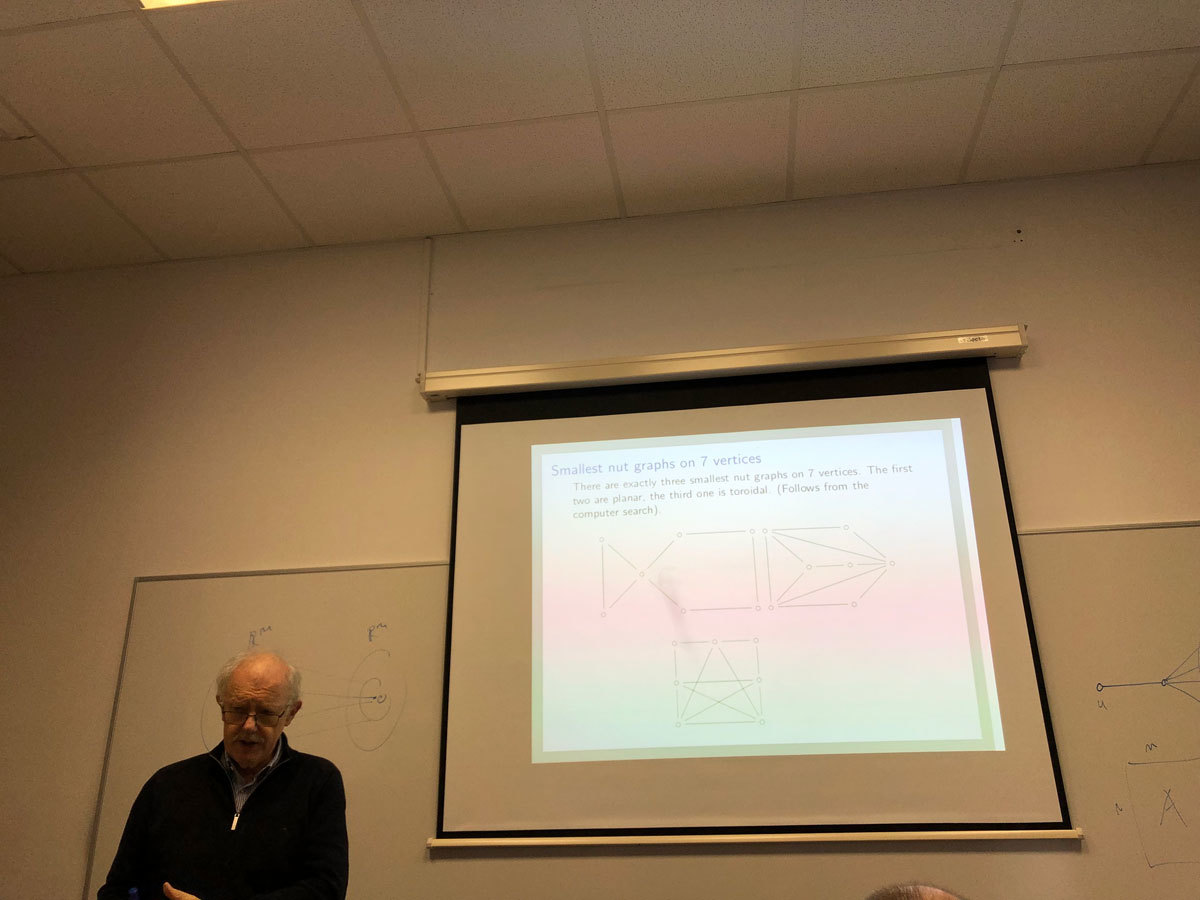
Regular nut graphs and the Fowler extension
A nut graph is a singular graph of nullity one with a kernel eigenvector having no component equal to 0. We attack the following problem. For each valence d, determine all values of n such that a regular, d-valent nut graph of order n exists. We solve this problem completely for d \leq 4. The main tool in our approach is the Fowler extension of a graph. If time permits we will also give a demonstration of a short sagemath program that tests whether a given graph is a nut graph. This talk is based on the work in progress with John Baptist Gauci and Irene Sciriha. In the proof of case d=4 the help of Patrick Fowler and Nino Bašić is acknowledged.