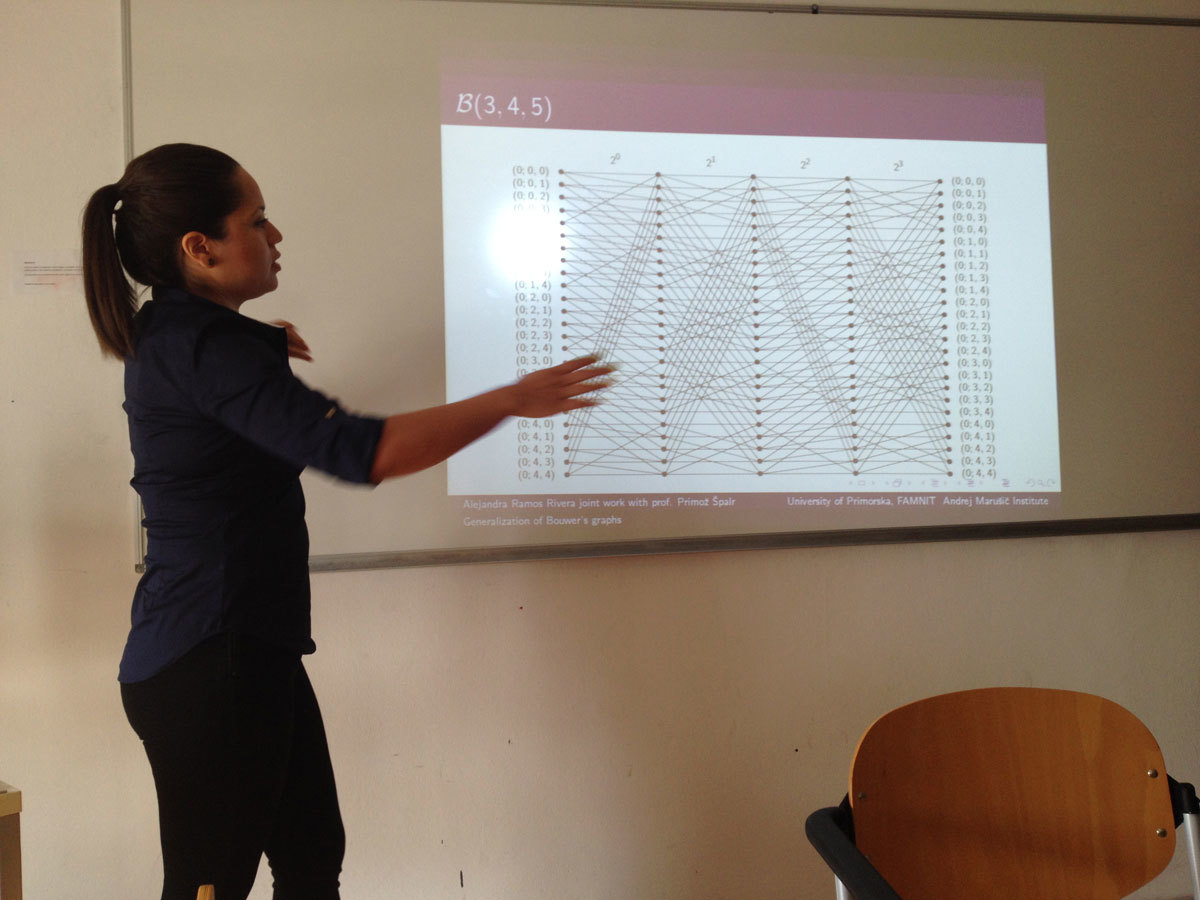
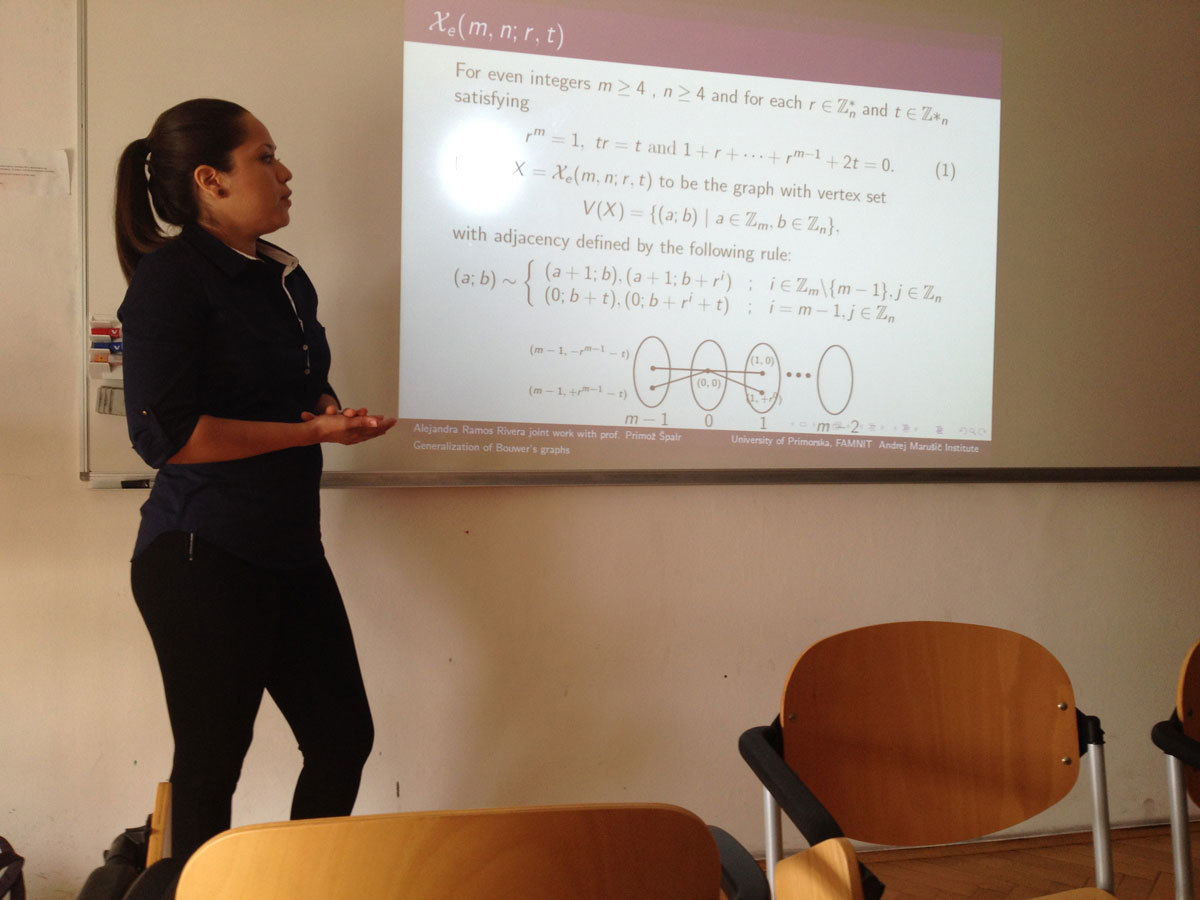Bouwer proved that there exists a half-transitive graph of every even valency greater that 2, by giving a contruction for a family of graphs now known as B(k,m,n). Recently, it was proved by M. Conder and A. Žitnik which of Bower’s graphs are half-arc-transitive.
Let D_G(X) be one of the two opposedly oriented digraphs associated with a half-transitive graph X with respect to the action of Aut(X). Two arcs are related if they have the same initial vertex (tail), or the same terminal vertex (head). The subgraphs consisting of equivalence classes of directed edges of this relation are called alternets.
Let {\cal A} = {A_i | i\in {1, 2, … ,m}} be the set of alternets in X and for each i\in {1, 2, . . . ,m} define H_i to be the set of all vertices at the heads of arcs in A_i\in{\cal A}, and T_i be the set of all vertices at the tail of arcs in A_i. If H_i = T_j for some i, j\in {1, 2, … ,m}, then X is said to be tightly attached. Tightly attached graphs with valency 4 were classified by P. Šparl and D. Marušič.
In this talk a family of tightly attached half-transitive graphs with valency 2k is introduced as a generalization of the Bouwer’s graphs.
Based on joint work with Primož Šparl.