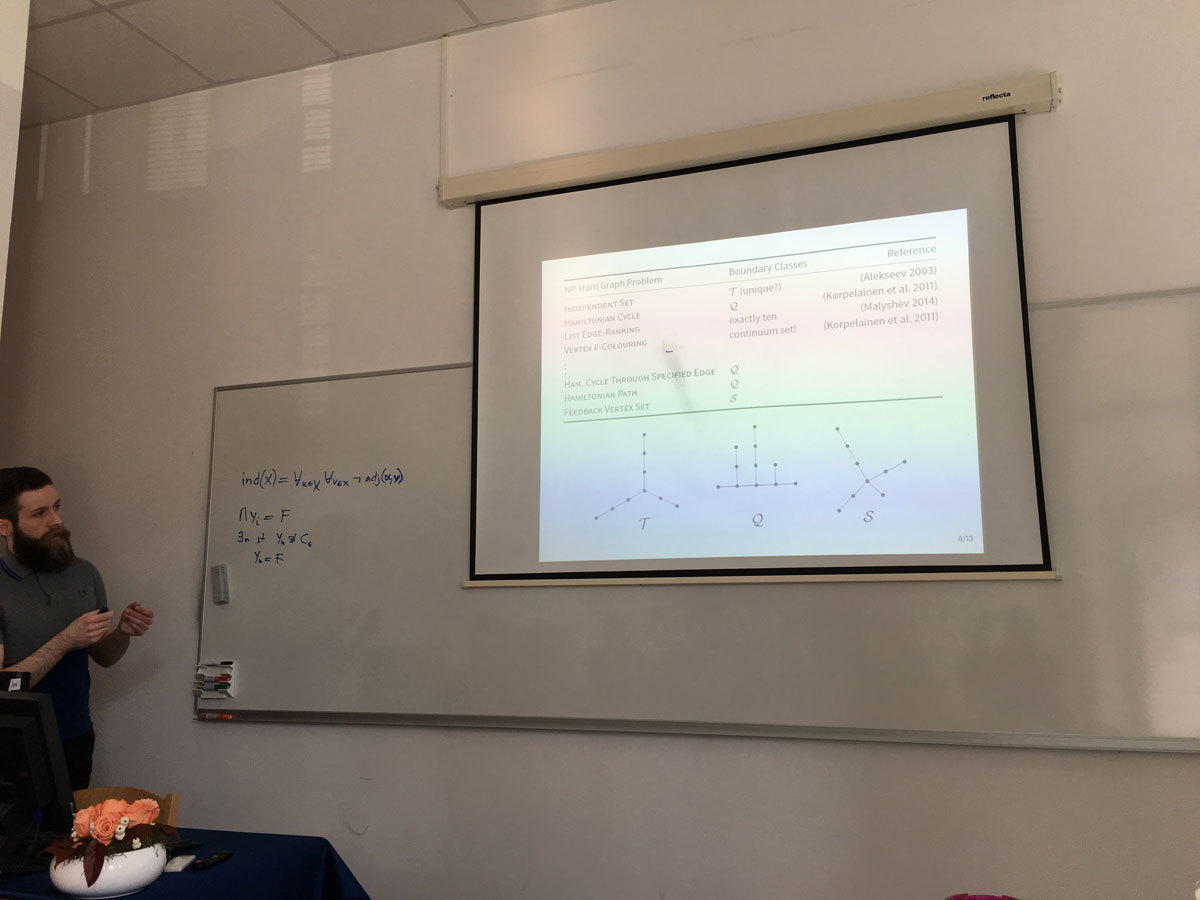
Many NP-hard graph problems remain NP-hard even for restricted classes of graphs, while they become polynomial-time solvable when further restrictions are applied. It is therefore natural to ask when a certain “hard” graph problem becomes “easy”: Is there any “boundary” separating “easy” and “hard” instances? Alekseev considered this question in the case the instances are hereditary classes of graphs.

Given a graph problem Pi, a hereditary class of graphs X is Pi-hard if Pi is NP-hard for X, and Pi-easy if Pi is solvable in polynomial time for graphs in X. He introduced the notion of Pi-boundary class, playing the role of the “boundary” separating Pi-hard and Pi-easy instances, and showed that a finitely defined (hereditary) class is Pi-hard if and only if it contains a Pi-boundary class. Moreover, he determined a boundary class for Independent Set, the first result in the systematic study of boundary classes for NP-hard graph problems. 

In the talk, I will review some known results and present new boundary classes for some problems involving non-local properties, like Hamiltonian Path and Feedback Vertex Set.